1. はじめに – ROC解析の問題点-
今日では,さまざまな放射線医用画像の領域で用いられるようになったROC解析ですが,ROC解析が世に出た当初から,言われ続けている問題点がROC解析にはいくつかあります.それらの中には,病変のあるなしを判定しているにかかわらず,観察者はその位置を示さなくても良いので,もし観察者が間違って同じ画像の中の違う場所を病変と思って“病変がある”と回答した場合でも,それは正しい反応(True Positive Response)と見なされる,ということや,一つの試料に信号(病変)は一つと限定されているので,実際には複数存在することの多い臨床例を用いることができない,ということの2点が含まれます.実際には,前者のようなケースは試料の数を増やすことによって影響が小さくなりますし,ROC実験を行う場合に観察者に実験試料の性質(特異性)について十分な説明を行うことで,後者のバイアスを減らすことが可能です.しかしながら,昨今のように,より実際の臨床に近い状況(設定)での評価が求められるようになってくると,そういったROC解析が抱える問題点を無視してばかりもいられなくなってきました.そこで,最近はそれらのROC解析の問題点を補うという意味で,LROC(ROC-type curve for task of detection and localization)[1]とFROC(free-response receiver operating characteristic)[2-4]という2つの解析法が以前よりも頻繁に話題に上がるようになってきました.
LROCはROC解析を開発したのと同じシカゴ大学のグループによって開発された解析法で,理論的背景はROC解析とほぼ同じと考えられます.しかし,FROC解析は名前は似ているものの,ROC解析とはだいぶ内容が異なっており,理論的背景や表示法がROC解析とは異なります.ここで注意していただきたいのは,どちらの解析法も,ROC解析と同じくらい古くからあるのに,ROC解析ほど普及していない,ということです.その理由は,このどちらの解析法もROC解析のように,ROC曲線のカーブフィッティングを行うための統計的推定法や,曲線間の統計的有意差の検定を行う手法が確立していないためだと思われます.確かに,LROC解析とFROC解析のどちらについても,それらの手法を開発,提案する論文が報告されていますが[5,6],それらはいずれもまだ確証されたものではありません.どちらの解析法の場合も,一番の問題点は,曲線を推定するのに用いるデータ点が,観察者によって異なるというところにあります.つまり,ROC解析では,同じ試料を用いた観察者実験であれば,評価点の数も対象もすべての観察者について同一ですが,上記の2つの解析法では観察者によって,データの数や対象が違ってしまう可能性が高くなります(もちろん,まったく同じになる場合もあります).そのため,現時点においては,観察者実験にLROCまたはFROC解析だけを単独で用いることには,統計的有意差検定が困難である,というROC解析よりも大きな問題点があります.
そこでこれらのジレンマを解決するために,シカゴ大学のわれわれの研究グループでは,以前から通常のROC解析の観察者実験を行う際に,観察者に病変の位置を示してもらう方法を採用し,ROC解析と同時にLROC解析のための実験も行うようにしています.つまり,ROC解析で必要十分なデータを求め,統計的有意差検定を行い,その上に,さらにROC解析のデータを補足する意味で,LROC曲線を計算して示す,という2段構えの実験を行っています.今回のUsers Group Newsでは,多くの方にこういった実験方法を学んでいただくために,まず,簡単にLROCの理論について述べ,その後に,通常のROC実験データと観察者が示した位置情報から,ROCKITといったROCカーブフィッティングプログラムを応用して,LROC曲線をプロットする方法について解説します.
2. LROC解析の理論[1]
ROC解析では,実際に存在する信号sについて,正しく信号Sが存在すると検出する確率PD(S|s) [真陽性率 (TPF: True Positive Fraction) ] を,判断基準という閾値を変化させて求めています.しかし,LROCでは,実際に存在する信号sについて,正しい位置CLで,正しく信号Sであると検出する確率PDL(S,CL|s)と,間違った位置ILで,正しく信号Sが存在すると検出する確率PDL(S,IL|s)の2つを考慮しています.ここで,ROC解析とLROC解析のそれぞれの確率は,以下の式で関係付けることが出来ます.
PD(S|s)=PDL(S,CL|s)+PDL(S,IL|s) — (1)
LROC解析において,実際に信号が存在するにかかわらず,位置の検出が間違っていた試料のスコアは,”間違って信号が存在しない” (FN: False Negative)と判定した結果として見なされます.そして,そのFNの確率は偽陰性率(FNS:False Negative Fraction)で定義されており,これがPDL(S,IL|s)に同じ意味を持ちます.つまり,刺激-反応マトリックスの理論においては,ROC曲線の縦軸を示すTPFは,TPF=1-FNFで定義されていて,通常のROC解析ではFNF=0で,TPFは1.0で収束するのですが,LROC解析では,前述のようにFNFは0ではなく,通常は0以上の値となりますので,LROC曲線の縦軸のTPFは,ほとんどの場合,TPF<1.0となります.もう少し具体的に述べるならば,100枚の信号像があった場合,ROC解析では,最終的にそこに含まれる100個の信号全部が検出されたと見なして計算されるので,最終的なTPF(感度)は1.0(100%)になるのですが,LROC解析の場合は,位置が正しく検出されなかった信号は,TPFにはカウントされませんので,例えば,100個のうち,10個の信号の位置が間違っていたとしたら,最終的なTPFは,0.9にしかなりません.
3. ROC解析ソフトを用いたLROC曲線の推定
通常のROC曲線をソフトウエア(ROCKIT)を用いて推定する場合,ROCKITで算出されるTPFは,前述の(1)式に示したPD(S|s)の積分値を,信号を含む試料数で標準化したものとなります.そして,同様にLROC解析で算出するTPFは,PDL(S,CL|s)の積分値を信号を含む試料数で標準化したものとなります.しかし,LROCにおけるPDL(S,CL|s)も,ROC解析におけるPD(S|s)と同様に正規分布になるということが,理論上では仮定されていますので,両正規分布ROC解析の理論を用いてカーブフィッティングを行うことは可能です.つまり,前述の例を用いるとすれば,100枚の信号像を用いた実験で,正常像も100枚とすると,ROC曲線を計算する場合には,信号像100+正常像100のすべての画像に対する評価点を用いて計算し,LROC曲線を計算する場合には,その下準備として,まず,位置が間違っていた10枚の信号像の評価点だけを除いた,信号像90+正常像100の画像に対する評価点を用いて通常のROC曲線を計算するようになります.これだけではわかりにくいと思われますので,ROCKITを用いてLROC曲線のカーブフィッティングおよび面積の計算する方法を,以下に順を追って説明します.
A) 通常のROC評定実験を行う場合に,各画像に対する評価点(信号のあるなしの判断基準)に加えて,信号の位置を観察者に指定してもらいます(明かに信号がないと観察者が思った場合でも,どこか1箇所を選んでもらうようにします).この場合,位置の情報は,画像を読影しているモニタ上(またはフィルム上)で記録できるような方法が望ましいですが,それが困難な場合は,試料のサイズに応じて,試料全体を4分割,9分割,16分割にして,そのセグメント番号で回答を得るという方法もあります.
B) 全部の信号像に与えられた位置のデータから,位置の検出が間違っている試料の数をカウントし,また,それらの画像の評価点を信号像の評価点データから削除します.
C) 位置間違い評価点データ削除後の信号像の評価点データと,全部の正常像の評価点データをROCKITに入力して,通常のROC曲線のカーブフィッティングを行います.
D) 算出されたTPFのデータ(この時点では,FPF=1.0のときにTPF=1.0となっている通常のROC曲線のデータです)に(T-D)/Tの値を乗じて,LROC曲線のTPF値を求めます.ここで,Tは全信号像の数,Dは位置検出が間違っていた信号像の枚数(=削除したデータ数)を表します.
E) LROC曲線下の面積(これをAZと読んで良いのかどうかは不明.たぶん不適当?)を算出したい場合には,これらのTPF値を用いて,台形近似もしくはWilcoxon近似で面積を求めます.
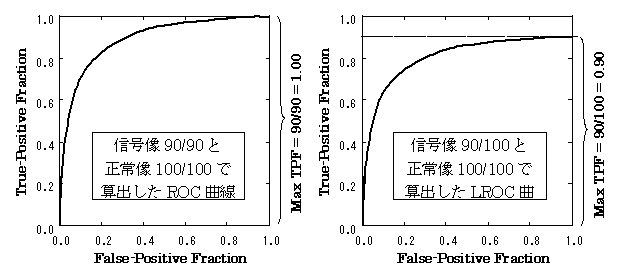
以上の方法で,LROC曲線を得るためのデータが得られます.この方法で得られるROC曲線とLROC曲線の関係を示したのがFig.1です.LROCのTPFが到達する値はFNと判定された試料のデータ数によって決まるので,最初にTPF=1.0となることを仮定して,ROC曲線のカーブフィッティングを行い,次に全体の値を(1-FNF)で補正して,LROC曲線を求めるという方法です.
4. まとめ
最後にもう一度思い出していただきたいのは,ここで示したLROC曲線の算出法はあくまで簡便法であって,個人個人のLROC曲線を算出する方法としては間違っていませんが,これらのLROC曲線の面積で統計的有意差検定を行ったり,観察者間の平均のLROC曲線を求める場合には,十分な配慮が必要であるということです.つまり,最初にも述べたように,観察者一人一人のLROC曲線は,すべて違うものである可能性が高いので,それらを平均したり,検定の対象に用いる場合には,そういったことを十分に理解する必要があるということと,さらにその手法を説明する場合には,そういった条件を正確に記述する必要があるということです.実際のところ,統計的検定はROC曲線間のもので十分だと思いますし,各観察者についてROC曲線とLROC曲線を示すことができれば,それだけでROC解析が抱えている問題点の一つを補うことができます.あくまで,このLROC解析はROC解析の問題点を補うためのものである,という点を理解していただけたらと思います.
今回はLROC解析だけについて解説を行いましたが,近いうちに今度はFROC解析についても解説を行いたいと思っています.
-参考文献-
[1] Stuart J, Starr BS, Metz CE, et.al.: Visual Detection and Localization of Radiographic Images, Radiology, 116, 533-538,1975.
[2] Bunch PC, Hamilton JF, Sanderson GK, and Simmons AH: A Free Response Approach to the Measurement and Characterization of Radiographic Observer Performance, SPIE, 127, 124-135, 1977.
[3] Chakraborty DP, Breatnach EA, Yester MV, et.al.: Digital and conventional chest Imaging: a modified ROC study of observer performance using simulated nodules. Radiology, 158, 35-39, 1986.
[4] Chakraborty DP, Winter LH.: Free-Response Methodology: Alternative Analysis and a New Observer-Performance Experiment. Radiology, 174, 873-881, 1990.
[5] Swensson RG: Unified measurement of observer performance in detecting and localizing target objects on images. Med Phys. 23, 1709-25, 1996.
[6] Chakraborty DP: Statistical power in observer-performance studies: comparison of the receiver operating characteristic and free-response methods in tasks involving localization. Acad Radiol. 9, 147-56, 2002.