今回のUsers Group Newsでは,皆さんからの質問にもよく出てくる,平均のROC曲線の求め方を取り上げたいと思います.
複数の観察者から得られたROC曲線の,平均のROC曲線を求める場合には,アベレージ法とプール法があり,通常の場合はアベレージ法を使用するように推奨しています.このことについては,過去のQ&Aでも説明していますが,その理由は何なのか?ということまで理解している方は少ないように思われます.また,あまり理解せずに(よく知らずに)プール法で平均のROC曲線を求めている場合が時折,研究発表などで見かけられます.平均のROC曲線を求める2つの方法の違いによって,結果に大きな差が生じることは,そう多くはありませんが,場合によっては,その違いが決定的な差を生じさせている可能性があります.そこで,ここでは具体的な例を示して,アベレージ法とプール法にどのような違いがあり,どうしてアベレージ法を使う方が良いのか,という点について解説したいと思います.
まず,最初にアベレージ法とプール法の計算方法とその結果の違いを説明するために,1つのROC実験の結果を想定します.そして,このROC実験は,胸部の腫瘤陰影の検出を目的として,3人の放射線科医(A,B,C)によって行われた,と仮定します.この実験のために用意された観察試料(胸部単純X線像)の枚数は, 信号あり10枚,信号なし10枚で,読影実験は連続確信度法(最大スコア:50)で行われたものとします.ここで注意していただきたいのですが,この仮想のデータは,あくまで平均のROC曲線の求め方の違いを説明するために想定したもので,実際の場合には,観察者の数も試料枚数も,この数よりも多くすることが必要ということを理解してください.Table1に, 20枚の試料について3人の放射線科医から得られたスコアを示します.ここでは,3人の観察者について,Aは自分の読影能力に自信のある熟練した放射線科医,Bは,経験はあるけれども自分の診断に非常に慎重な放射線科医,Cは経験の少ない放射線科医,という想定でスコアを作成しました.これはあくまで,私のこれまでの個人的な経験から得た知識ですが,Aのタイプの観察者は,観察者の判断が正しい正しくないに関わらず,スコアが両極端(最大値と最小値)に離れる場合が多く,Bのタイプの観察者の場合は,逆に両極端のスコアが少なくなる傾向にあります.AとBの場合はスコアのばらつきの程度が違いますが,各試料に付いての判定は似ている傾向を示す場合が多いですが,Cの観察者は,時として,AやBとはまったく逆の判定のスコアを示すことがあります.では,これらのスコアについて,実際にアベレージ法とプール法で平均のROC曲線を求めて,その差を検討してみることにしましょう.
| 観察者 | 信号(腫瘤)なしの試料に対するスコア | 信号(腫瘤)ありの試料に対するスコア | A | 1 | 6 | 39 | 2 | 5 | 41 | 8 | 12 | 7 | 3 | 48 | 17 | 4 | 49 | 50 | 12 | 46 | 10 | 44 | 50 | B | 7 | 8 | 24 | 4 | 6 | 30 | 9 | 16 | 5 | 1 | 31 | 16 | 29 | 42 | 39 | 2 | 35 | 14 | 28 | 43 | C | 9 | 35 | 11 | 5 | 2 | 45 | 3 | 4 | 15 | 7 | 40 | 6 | 44 | 46 | 49 | 39 | 10 | 1 | 24 | 48 |
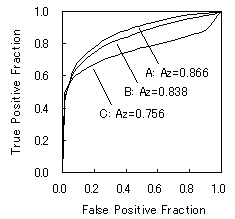
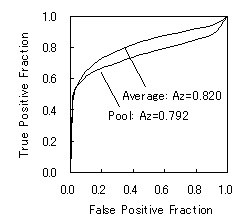
アベレージ法による平均のROC曲線の求め方は,まず各観察者についてROC曲線を推定します.現在では,このROC曲線の推定には,このUsers Groupでも紹介しているROCKITを用いるのがもっとも適当と思われますので,ここでもROCKITを用いて3人のROC曲線を推定します.Fig.1に示したのが,ROCKITを用いて得られた3人のROC曲線とROC曲線下の面積AZです.ROCKITでは,ROC曲線をプロットするための座標が,決まったFPF(0.0~1.0)について与えられますので,アベレージ法による平均のROC曲線は,各FPFについてTPFの平均を算出することで求められます(Fig.2).そして,この平均のROC曲線のAZは,3人のAZの平均値にほぼ等しく,この場合は,0.820になります.
一方,プール法による平均のROC曲線は,3人の評定実験で得られたスコアをひとまとめにしてROC曲線の推定を行います.つまり,Table 1に示したデータの,信号(腫瘤)なしの試料に対するスコアと信号(腫瘤)ありの試料に対するスコアをまとめてROCKITへ入力することで平均のROC曲線が推定されます.この方法で得られた平均のROC曲線をFig.2に示します.図からわかるように,プール法で推定したROC曲線は,アベレージ法よりも下になり,AZもアベレージ法よりは小さくなっています(AZ=0.792).
 |
 |
ここで示した例では,アベレージ法とプール法の間に比較的大きな差が生じましたが,試料数が多い場合は,差はもう少し小さいと予想されます.ただし,つねにプール法で求めたROC曲線はアベレージ法よりも下になり,AZは小さい値となります.これは,各観察者のスコアの正規分布が観察者によって異なるためで,各観察者について最適な正規分布を推定している両正規ROC解析では,3人の観察者のスコアの正規分布が一致した時にのみ,アベレージ法とプール法の両者で得られたROC曲線が同一になります.したがって,平均のROC曲線を求める場合には,アベレージ法を用いた方が,より正確な曲線が得られるという事になります.皆さんの中には,少ない試料数の場合,プール法で平均を求めた方がデータの精度が向上すると考えている方がおられるかもしれませんが,それは大きな誤解です.今回の例でもわかるように,試料枚数の少ない場合ほど,アベレージ法とプール法の差が大きくなります.
また,2つの平均ROC曲線間の差を統計的に検定する場合も,アベレージ法の方がAZを用いてt検定を実行できるという点で有利です(Q&A参照).そして,プール法で得られたデータに関しては,今のところ適当な検定方法がありません.では,プール法は何のためにあるのか?という疑問が生じるかもしれません.その答えは,プール法でしか平均のROC曲線を求められない場合があるからです.ただし,これは非常に特殊な場合に限られますので,今回は説明をしません.もし,実際にROC実験を行って,どうしてもプール法でしか平均のROC曲線が求められない,という状況に遭遇しましたら,その時は,質問のメールをUsers Groupまでお寄せください.